树状数组提高篇

概述

主要记录各种树状数组的例题

例1.【模板】树状数组 (单点修改，区间查询)

题目链接

题目描述

如题，已知一个数列，你需要进行下面两种操作：

将某一个数加上 $x$
求出某区间每一个数的和

输入格式

第一行包含两个正整数 $n,m$，分别表示该数列数字的个数和操作的总个数。

第二行包含 $n$ 个用空格分隔的整数，其中第 $i$ 个数字表示数列第 $i$ 项的初始值。

接下来 $m$ 行每行包含 $3$ 个整数，表示一个操作，具体如下：

1 x k 含义：将第 $x$ 个数加上 $k$
2 x y 含义：输出区间 $[x,y]$ 内每个数的和

输出格式

输出包含若干行整数，即为所有操作 $2$ 的结果。

输入样例

输出样例

14
16

数据范围

对于 $30\%$ 的数据，$1 \le n \le 8$，$1\le m \le 10$

对于 $70\%$ 的数据，$1\le n,m \le 10^4$

对于 $100\%$ 的数据，$1\le n,m \le 5\times 10^5$

样例说明

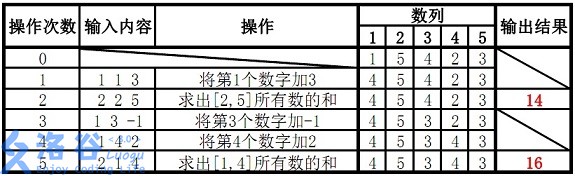
故输出结果14、16

题解

单点修改，区间查询模板题

代码

#include<bits/stdc++.h>

using namespace std;

int tr[500005];
int n,m;

int lowbit(int x)
{
    return x&-x;
}

void add(int x, int c)
{
    for (int i = x; i <= n; i += lowbit(i)) tr[i] += c;
}

int sum(int x)
{
    int res = 0;
    for (int i = x; i; i -= lowbit(i)) res += tr[i];
    return res;
}

int main()
{
    int k;
    cin>>m>>n;
    for(int i=1;i<=m;i++)
    {
        cin>>k;
        add(i,k);
    }
    int command,a,b;
    for(int i=1;i<=n;i++)
    {
        cin>>command>>a>>b;
        if(command==1) add(a,b);
        if(command==2) cout<<sum(b)-sum(a-1)<<endl;
    }
    return 0;
}

例2.【模板】树状数组 (区间修改,单点查询)

题目链接

题目描述

如题，已知一个数列，你需要进行下面两种操作：

将某区间每一个数加上 $x$；
求出某一个数的值。

输入格式

第一行包含两个整数 $N$、$M$，分别表示该数列数字的个数和操作的总个数。

第二行包含 $N$ 个用空格分隔的整数，其中第 $i$ 个数字表示数列第 $i $ 项的初始值。

接下来 $M$ 行每行包含 $2$ 或 $4$个整数，表示一个操作，具体如下：

操作 $1$：格式：1 x y k 含义：将区间 $[x,y]$ 内每个数加上 $k$；

操作 $2$：格式：2 x 含义：输出第 $x$ 个数的值。

输出格式

输出包含若干行整数，即为所有操作 $2$ 的结果。

输入样例

输出样例

6
10

样例解释

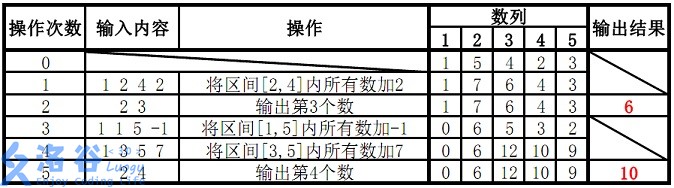
故输出结果为 6、10。

数据规模与约定

对于 $30\%$ 的数据：$N\le8$，$M\le10$；

对于 $70\%$ 的数据：$N\le 10000$，$M\le10000$；

对于 $100\%$ 的数据：$1 \leq N, M\le 500000$，$1 \leq x, y \leq n$，保证任意时刻序列中任意元素的绝对值都不大于 $2^{30}$。

题解

区间修改，单点查询模板题，维护差分数组即为区间修改，前缀和即为单点查询

若修改区间为$[l,r]$，同时加上$x$

则操作如下：

$add(l, x)$
$add(r+1, -x)$

代码

#include<bits/stdc++.h>
using namespace std;

const int N=5e5+5;

int a[N],cha[N],tr[N];
int n,m;

int lowbit(int x){return x&-x;}

void add(int x, int c)
{
    for (int i = x; i <= n; i += lowbit(i)) tr[i] += c;
}

void update(int l,int r,int x)
{
    add(l,x);
    add(r+1,-x);
}

int sum(int x)
{
    int res = 0;
    for (int i = x; i; i -= lowbit(i)) res += tr[i];
    return res;
}

int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
        add(i,a[i]-a[i-1]); // 维护的是差分数组
    }
    int op,a,b,c;
    for(int i=1;i<=m;i++)
    {
        cin>>op;
        if(op==1)
        {
            cin>>a>>b>>c;
            update(a,b,c);
        }
        else
        {
            cin>>a;
            cout<<sum(a)<<endl;
        }
    }
    return 0;
}

例3.楼兰图腾

题目描述

在完成了分配任务之后，西部 314 来到了楼兰古城的西部。

相传很久以前这片土地上(比楼兰古城还早)生活着两个部落，一个部落崇拜尖刀(V)，一个部落崇拜铁锹(∧)，他们分别用 V 和 ∧ 的形状来代表各自部落的图腾。

西部 314 在楼兰古城的下面发现了一幅巨大的壁画，壁画上被标记出了 $n$ 个点，经测量发现这 n 个点的水平位置和竖直位置是两两不同的。

西部 314 认为这幅壁画所包含的信息与这 n 个点的相对位置有关，因此不妨设坐标分别为$(1,y_1),(2,y_2),…,(n,y_n)$，其中 $y_1∼y_n$ 是 $1$ 到 $n$ 的一个排列。

西部 314 打算研究这幅壁画中包含着多少个图腾。

如果三个点 $(i,y_i),(j,y_j),(k,y_k)$ 满足 $1≤i<j<k≤n$ 且 $y_i>y_j,y_j<y_k$，则称这三个点构成 V 图腾;

如果三个点 $(i,y_i),(j,y_j),(k,y_k)$ 满足 $1≤i<j<k≤n$ 且 $y_i<y_j,y_j>y_k$，则称这三个点构成 ∧ 图腾;

西部 314 想知道，这 $n$ 个点中两个部落图腾的数目。

因此，你需要编写一个程序来求出 V 的个数和 ∧ 的个数。

输入格式

第一行一个数 $n$。

第二行是 $n$ 个数，分别代表 $y1，y2,…,yn$。

输出格式

两个数，中间用空格隔开，依次为 V 的个数和 ∧ 的个数。

数据范围

$对于所有数据，n≤200000，且输出答案不会超过 int64。$

$y_1∼y_n 是 1 到 n 的一个排列。$

输入样例

5
1 5 3 2 4

输出样例

5
1 5 3 2 4

题解

遍历每个点，对于第$i$个点，若前方比他大的由$a$个，后方比他大的有$b$个，则可以知道对于这个点能产生$a*b$个V

同理可得∧的数量

树状数组在这里的作用就是单点修改，区间查询

代码

#include <iostream>
#include <cstring>
#include <algorithm>

typedef long long LL;

using namespace std;
const int N=2e5+5;
int tree[N];
int great[N],lower[N];
int a[N];
int n;
int lowbit(int x){return x&-x;}
void add(int x,int c)
{
    for(int i=x;i<=n;i+=lowbit(i)) tree[i]+=c;
}
int sum(int x)
{
    int res=0;
    for(int i=x;i;i-=lowbit(i)) res+=tree[i]; 
    return res;
}
signed main()
{
    cin.tie(0);
    cout.tie(0);
    ios::sync_with_stdio(0);
    cin>>n;
    LL res1=0,res2=0;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
        add(a[i],1);
        great[i]=sum(n)-sum(a[i]);
        lower[i]=sum(a[i]-1);
    }
    for(int i=1;i<=n;i++)
    {
        res1+=1LL*great[i]*(sum(n)-sum(a[i])-great[i]);
        res2+=1LL*lower[i]*(sum(a[i]-1)-lower[i]);
    }
    cout<<res1<<" "<<res2<<endl;
    return 0;
}

例4.谜一样的牛

题目链接

题目描述

有 $n$ 头奶牛，已知它们的身高为 $1∼n$ 且各不相同，但不知道每头奶牛的具体身高。

现在这 $n$ 头奶牛站成一列，已知第 $i$ 头牛前面有 $A_i$ 头牛比它低，求每头奶牛的身高。

输入格式

第 $1$ 行：输入整数 $n$。

第 $2..n$ 行：每行输入一个整数 $A_i$，第 $i$ 行表示第 $i$ 头牛前面有 $A_i$ 头牛比它低。（注意：因为第 1 头牛前面没有牛，所以并没有将它列出）

输出格式

输出包含 $n$ 行，每行输出一个整数表示牛的身高。

第 $i$ 行输出第 $i$ 头牛的身高。

数据范围

$1≤n≤10^5$

输入样例

输出样例

题解

首先，我们发现最后一头牛的位置是可以直接确定下来的

这里给了我们一个倒着来的思路

那倒数第二个牛的位置怎么算呢？

如果最后一头牛的位置为$A[n]+1$，则倒数第二头牛是$n$头牛除去第$A[n]+1$高位置的牛，剩下的牛中第$A[n-1]+1$高的

我们可以构造一个$01$串,$1$表示当前位置的牛并未被选择

则第$x+1$高就是前缀和为$x+1$

前缀和可以通过树状数组维护

又由于前缀和单调不减，这里又发现了二段性，于是可以考虑二分

所以本题只需要从后往前遍历，每次二分查找前缀和为$A[i]+1$的位置即可

代码

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int a[N];
int n;
int tree[N];
int lowbit(int x){return x&-x;}
void add(int x,int c){for(int i=x;i<=n;i+=lowbit(i)) tree[i]+=c;}
int sum(int x)
{
    int res=0;
    for(int i=x;i;i-=lowbit(i)) res+=tree[i];
    return res;
}
vector<int> res;
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        if(i>=2) cin>>a[i];
        add(i,1); // 初始都为1，表示每头牛都在
    }
    for(int i=n;i>=1;i--)
    {
        int l=1,r=n;
        while(l<r)
        {
            int mid=(l+r)>>1;
            if(sum(mid)>=a[i]+1) r=mid;
            else l=mid+1;
        }
        res.push_back(l);
        add(l,-1); // 从现有牛中删去
    }
    reverse(res.begin(),res.end());
    for(int i=0;i<res.size();i++) cout<<res[i]<<endl;
    return 0;
}

树状数组 提高篇

概述

例1.【模板】树状数组 (单点修改，区间查询)

题目描述

题解

代码

例2.【模板】树状数组 (区间修改,单点查询)

题目描述

题解

代码

例3.楼兰图腾

题目描述

题解

代码

例4.谜一样的牛

题目描述

题解

代码

树状数组提高篇