逆元

概述

如果一个线性同余方程\(ax≡1(mod \ b)\),则称\(x\)是\(a\ mod \ b\)的逆元，记作\(a-1\)。(当\(a⊥b\)时才有逆元)

---

扩欧求逆元

代码模板

void exgcd(int a, int b, int& x, int& y) {  
    if (b == 0) {  
    x = 1, y = 0;  
    return;  
    }  
    exgcd(b, a % b, y, x);  
    y -= a / b * x;  
}  

---

费马小定理求逆元

费马小定理：

若存在整数\(a,p\)且\(gcd(a,p)=1\),即二者互为质数，则有\(a^{p-1}≡1(mod \ p)\)。此时 \(a^{p-2}\)是\(a\mod\ p\)的逆元 由于p一般很大，用快速幂来求

代码模板

ll qpow(ll a,ll n)  
{  
    ll ans=1;  
    while(n)  
    {  
        if(n%2) ans=ans*a%mod;  
        a=a*a%mod;  
        n/=2;  
    }  
    return ans;  
}  

---

线性求逆元

求1-n的逆元

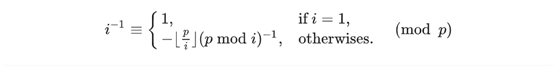
代码模板

inv[1] = 1;  
for (int i = 2; i <= n; ++i) {  
    inv[i] = (long long)(p - p / i) * inv[p % i] % p;  
}  

求给定n个数的逆元

首先计算\(n\)个数的前缀积，记为\(pre[i]\)，然后使用快速幂或扩展欧几里得法计算\(pre[n]\) 的逆元，记为$Inv[n] $。

因为\(Inv[n]\)是\(n\)个数的积的逆元，所以当我们把它乘上\(a[n]\)时，就会和\(a[n]\)的逆元抵消，于是就得到了\(a[1] \(到\)a[n-1]\)的积逆元，记为\(Inv[n-1]\)。

同理我们可以依次计算出所有的\(Inv[i]\)，于是\(a[i-1]\)就可以用\(pre[i-1] \times Inv[i]\)求得。

所以我们就在\(O(n+logp)\)的时间内计算出了\(n\)个数的逆元。

代码模板

void init()  
{  
    pre[0] = 1;  
    for (int i = 1; i <= n; ++i) pre[i] = pre[i - 1] * a[i] % p;  
    inv[n] = qpow(pre[n], p - 2);  
    // 当然这里也可以用 exgcd 来求逆元,视个人喜好而定.  
    for (int i = n; i >= 1; --i) inv[i - 1] = inv[i] * a[i] % p;  
    for (int i = 1; i <= n; ++i) inv[i] = inv[i] * pre[i - 1] % p;  
}  

---

例1.乘法逆元2

题目入口

题目描述

这可能是一道模板题。

给定个正整数,求每个数在模意义下的乘法逆元。

提示：请使用高效的读入方式。

输入格式

第一行一个整数n。

第二行n个整数ai。

输出格式

一行一个数

输入样例

5
4 7 8 12 123456

输出样例

650798912

题解

求一堆数逆元模板题

代码

#include<bits/stdc++.h>  
using namespace std;  
typedef long long ll;  
const ll mod=1e9+7;  
const ll N=998244353;  
ll a[5000005];  
ll pre[5000005];  
ll qpow(ll a,ll n)  
{  
        ll ans=1;  
        while(n)  
        {  
            if(n&1) ans=(ans%mod)*(a%mod)%mod;  
            a=a*a%mod;  
            n/=2;  
        }  
        return ans;  
    }  

int read() {  
    int x=0,f=1;  
    char c=getchar();  
    while(c<'0'||c>'9'){if(c=='-') f=-1;c=getchar();}  
    while(c>='0'&&c<='9') x=x*10+c-'0',c=getchar();  
    return x*f;  
}  
ll inv[5000005];  
int main()  
{  
    int n;  
    scanf("%d",&n);  
    pre[0]=1;  
    ll ans=0;  
    for(int i=1;i<=n;i++)  
    {  
        a[i]=read();  
        pre[i]=pre[i-1]*a[i]%mod;  
    }  
    inv[n]=qpow(pre[n],mod-2);  
    for(int i=n;i>=1;i--) inv[i-1]=inv[i]%mod*a[i]%mod;  
    for(int i=1;i<=n;i++)  
    {  
        ans=ans*N%mod+inv[i]*pre[i-1]%mod;  
    }  
    printf("%lld\n",ans%mod);  
    return 0;  
}