单源最短路应用
概述
从图中的某个顶点出发到达另外一个顶点的所经过的边的权重和最小的一条路径,称为最短路径
解决问题有以下算法:
本章讲解最短路的例题
例1.选择最佳线路
题目链接
题目描述
有一天,琪琪想乘坐公交车去拜访她的一位朋友。
由于琪琪非常容易晕车,所以她想尽快到达朋友家。
现在给定你一张城市交通路线图,上面包含城市的公交站台以及公交线路的具体分布。
已知城市中共包含 n 个车站(编号1~n)以及 m 条公交线路。
每条公交线路都是 单向的,从一个车站出发直接到达另一个车站,两个车站之间可能存在多条公交线路。
琪琪的朋友住在 s 号车站附近。
琪琪可以在任何车站选择换乘其它公共汽车。
请找出琪琪到达她的朋友家(附近的公交车站)需要花费的最少时间。
输入格式
输入包含多组测试数据。
每组测试数据第一行包含三个整数 n,m,s,分别表示车站数量,公交线路数量以及朋友家附近车站的编号。
接下来 m 行,每行包含三个整数 p,q,t,表示存在一条线路从车站 p 到达车站 q,用时为 t。
接下来一行,包含一个整数 w,表示琪琪家附近共有 w 个车站,她可以在这 w 个车站中选择一个车站作为始发站。
再一行,包含 w 个整数,表示琪琪家附近的 w 个车站的编号。
输出格式
每个测试数据输出一个整数作为结果,表示所需花费的最少时间。
如果无法达到朋友家的车站,则输出 -1。
每个结果占一行。
数据范围
\(n≤1000,m≤20000,\)
\(1≤s≤n,\)
\(0<w<n,\)
\(0<t≤1000\)
输入样例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17 | 5 8 5
1 2 2
1 5 3
1 3 4
2 4 7
2 5 6
2 3 5
3 5 1
4 5 1
2
2 3
4 3 4
1 2 3
1 3 4
2 3 2
1
1
|
输出样例
题解
对于多起点到任意终点,我们可以建立一个虚拟的超级源点,这个点与所有起点的距离为0,最后只需要计算出这个超级源点到终点的距离即可
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71 | #include<bits/stdc++.h>
using namespace std;
int n,m,s;
const int N=1005,M=4e4+5;
int head[N],e[M],w[M],ne[M],idx=0;
void add(int a,int b,int c)
{
e[idx]=b;
w[idx]=c;
ne[idx]=head[a];
head[a]=idx++;
}
int dis[N];
bool vis[N];
typedef pair<int,int> PII;
priority_queue<PII,vector<PII>,greater<PII> >heap;
void djs(int s,int t)
{
while(heap.size()) heap.pop();
memset(vis,false,sizeof(vis));
memset(dis,0x3f,sizeof(dis));
dis[s]=0;
heap.push({0,s});
while(heap.size())
{
auto cur = heap.top();
heap.pop();
int pos=cur.second;
if(vis[pos]) continue;
vis[pos]=true;
for(int i=head[pos];i!=-1;i=ne[i])
{
int j=e[i];
if(dis[j]>dis[pos]+w[i])
{
dis[j]=dis[pos]+w[i];
heap.push({dis[j],j});
}
}
}
if(dis[t]==0x3f3f3f3f) cout<<"-1"<<endl;
else cout<<dis[t]<<endl;
}
int main()
{
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(0);
while(cin>>n>>m>>s)
{
idx=0;
memset(head,-1,sizeof(head));
for(int i=1;i<=m;i++)
{
int a,b,c;
cin>>a>>b>>c;
add(a,b,c);
}
int w;
cin>>w;
for(int i=1;i<=w;i++) // 超级源点
{
int a;
cin>>a;
add(0,a,0);
}
djs(0,s);
}
return 0;
}
|
例2.拯救大兵瑞恩
题目链接
题目描述
1944 年,特种兵麦克接到国防部的命令,要求立即赶赴太平洋上的一个孤岛,营救被敌军俘虏的大兵瑞恩。
瑞恩被关押在一个迷宫里,迷宫地形复杂,但幸好麦克得到了迷宫的地形图。
迷宫的外形是一个长方形,其南北方向被划分为 N 行,东西方向被划分为 M 列, 于是整个迷宫被划分为 N×M 个单元。
每一个单元的位置可用一个有序数对 (单元的行号, 单元的列号) 来表示。
南北或东西方向相邻的 2 个单元之间可能互通,也可能有一扇锁着的门,或者是一堵不可逾越的墙。
注意: 门可以从两个方向穿过,即可以看成一条无向边。
迷宫中有一些单元存放着钥匙,同一个单元可能存放 多把钥匙,并且所有的门被分成 P 类,打开同一类的门的钥匙相同,不同类门的钥匙不同。
大兵瑞恩被关押在迷宫的东南角,即 (N,M) 单元里,并已经昏迷。
迷宫只有一个入口,在西北角。
也就是说,麦克可以直接进入 (1,1) 单元。
另外,麦克从一个单元移动到另一个相邻单元的时间为 1,拿取所在单元的钥匙的时间以及用钥匙开门的时间可忽略不计。
试设计一个算法,帮助麦克以最快的方式到达瑞恩所在单元,营救大兵瑞恩。
输入格式
第一行有三个整数,分别表示 N,M,P 的值。
第二行是一个整数 k,表示迷宫中门和墙的总数。
接下来 k 行,每行包含五个整数,Xi1,Yi1,Xi2,Yi2,Gi:当 Gi≥1 时,表示 (Xi1,Yi1) 单元与 (Xi2,Yi2) 单元之间有一扇第 Gi 类的门,当 Gi=0 时,表示 (Xi1,Yi1) 单元与 (Xi2,Yi2) 单元之间有一面不可逾越的墙。
接下来一行,包含一个整数 S,表示迷宫中存放的钥匙的总数。
接下来 S 行,每行包含三个整数 Xi1,Yi1,Qi,表示 (Xi1,Yi1) 单元里存在一个能开启第 Qi 类门的钥匙。
输出格式
输出麦克营救到大兵瑞恩的最短时间。
如果问题无解,则输出 -1。
数据范围
\(|Xi1−Xi2|+|Yi1−Yi2|=1,\)
\(0≤Gi≤P,\)
\(1≤Qi≤P,\)
\(1≤N,M,P≤10,\)
\(1≤k≤150\)
输入样例
1
2
3
4
5
6
7
8
9
10
11
12
13
14 | 4 4 9
9
1 2 1 3 2
1 2 2 2 0
2 1 2 2 0
2 1 3 1 0
2 3 3 3 0
2 4 3 4 1
3 2 3 3 0
3 3 4 3 0
4 3 4 4 0
2
2 1 2
4 2 1
|
输出样例
样例解释
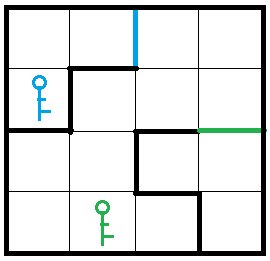
题解
若没有钥匙的限制,那这题就是普通的最短路问题,现在加上了钥匙,原来的f[i]已经不足以表示状态了,需要新开一维用来表示钥匙,注意到钥匙的数量很少,因此可以对其进行状态压缩,将二维坐标映射成一维之后,f[i][j]就表示达到当前在i,钥匙状态为j时的操作步数,最后的结果就是从f[s][0]到f[n*m][...]的最小步数,至于为什么钥匙状态未知,是因为我们只需要到达终点即可,转移过程如下:
- 有墙:不转移
- 有门无钥匙:不转移
- 有门有钥匙:正常转移
- 无门无墙:正常转移
- 是钥匙:转移时步数不变
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125 | #include<bits/stdc++.h>
using namespace std;
const int N=11, M=360, K= 1 << 10 ; // 对钥匙进行状态压缩
int n,m,p;
int head[N * N],e[M],w[M],ne[M], idx=0;
void add(int a,int b,int c)
{
e[idx]=b;
w[idx]=c;
ne[idx]=head[a];
head[a]=idx++;
}
typedef pair<int,int> PII;
int g[N][N];
int dis[N*N][K];
bool vis[N * N][K];
struct node_
{
int x;
int dis;
int key;
friend bool operator < (const node_ x,const node_ y)
{
return x.dis > y.dis;
}
};
priority_queue<node_> heap;
set<PII> edge;
int key[N * N];
void init()
{
memset(head,-1,sizeof(head));
for(int i=1,t=0;i<=n;i++)
for(int j=1;j<=m;j++)
g[i][j]=++t; // 二维映射成一维
}
int dir[4][2]={0,1,0,-1,1,0,-1,0};
void bulid()
{
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
for(int kk=0;kk<=3;kk++)
{
int a = i + dir[kk][0];
int b = j + dir[kk][1];
if (a < 1 || b < 1 || a > n || b > m) continue;
int ga = g[a][b], gb = g[i][j];
if (!edge.count({ga,gb})) add(ga, gb, 0); //没有墙则建长度为0的边,因为枚举上下左右,所以是有向边
}
}
void djs(int sx, int sy)
{
while(heap.size()) heap.pop();
memset(dis,0x3f,sizeof(dis));
dis[1][0] = 0;
heap.push({1, 0, 0});
while(heap.size())
{
auto cur = heap.top();
heap.pop();
int pos = cur.x,k = cur.key;
if (vis[pos][k]) continue;
vis[pos][k] = true;
if(pos == n*m)
{
cout<<dis[pos][k]<<endl;
return ;
}
if (key[pos]) // 当前是钥匙,转移时步数不变
{
int state = k | key[pos];
if (dis[pos][state] > dis[pos][k])
{
dis[pos][state] = dis[pos][k];
heap.push({pos, dis[pos][state], state});
}
}
for(int i = head[pos]; i != -1;i = ne[i])
{
int t = e[i];
if (w[i] && !((k >> w[i] - 1) & 1 )) continue; // 有门无钥匙不转移
if (dis[t][k] > dis[pos][k] + 1)
// 有门有钥匙或无门无墙转移
{
dis[t][k] = dis[pos][k] + 1;
heap.push({t, dis[t][k], k});
}
}
}
cout<<"-1"<<endl;
}
int main()
{
cin>>n>>m>>p;
int k;
cin>>k;
init();
for(int i=1;i<=k;i++)
{
int x1,y1,x2,y2,gg;
cin>>x1>>y1>>x2>>y2>>gg;
int a = g[x1][y1], b = g[x2][y2];
edge.insert({a,b}); // 墙或门的集合
edge.insert({b,a});
if(gg) // 是门的话存下来
{
add(a,b,gg);
add(b,a,gg);
}
}
bulid(); // 存没有门或墙的两个格
int s;
cin>>s;
for(int i=1;i<=s;i++)
{
int x,y,gg;
cin>>x>>y>>gg;
key[g[x][y]] |= (1 << gg - 1); // 一维状态存下钥匙
}
djs(1, 1);
return 0;
}
|
例3.最短路计数
题目链接
题目描述
给出一个 N 个顶点 M 条边的无向无权图,顶点编号为 1 到 N。
问从顶点 1 开始,到其他每个点的最短路有几条。
输入格式
第一行包含 2 个正整数 N,M,为图的顶点数与边数。
接下来 M 行,每行两个正整数 x,y,表示有一条顶点 x 连向顶点 y 的边,请注意可能有自环与重边。
输出格式
输出 N 行,每行一个非负整数,第 i 行输出从顶点 1 到顶点 i 有多少条不同的最短路,由于答案有可能会很大,你只需要输出对 100003 取模后的结果即可。
如果无法到达顶点 i 则输出 0。
数据范围
\(1≤N≤10^5,\)
\(1≤M≤2×10^5\)
输入样例
| 5 7
1 2
1 3
2 4
3 4
2 3
4 5
4 5
|
输出样例
题解
f[i]表示从起始点到i的最短路径的条数,转移状态如下:
- 当\(dis[j] > dis[u] + 1\)时:f[j] = f[u]
- 当\(dis[j] == dis[u] + 1\)时:f[j] += f[u]
- 当\(dis[j] < dis[u] + 1\)时:不更新
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67 | #include<bits/stdc++.h>
using namespace std;
const int N=1e5+5,M=4e5+5,mod=1e5+3;
int head[N],e[M],ne[M],idx=0;
void add(int a,int b)
{
e[idx] = b;
ne[idx] = head[a];
head[a] = idx++;
}
int dis[N];
bool vis[N];
int cnt[N]; // 记录条数
queue<int> q;
void djs(int s)
{
memset(dis,0x3f,sizeof(dis));
dis[s] = 0;
vis[s] = true;
cnt[s] = 1;
q.push(s);
while(q.size())
{
int pos = q.front();
q.pop();
vis[pos] = false;
for(int i=head[pos];i!=-1;i=ne[i])
{
int t = e[i];
if (dis[t] >= dis[pos] + 1)
{
if (dis[t] > dis[pos] + 1)
{
dis[t] = dis[pos] + 1;
cnt[t] = cnt[pos];
if (!vis[t])
{
vis[t] = true;
q.push(t);
}
}
else
{
cnt[t] += cnt[pos];
cnt[t] %= mod;
}
}
}
}
}
int main()
{
int n,m;
cin>>n>>m;
memset(head,-1,sizeof(head));
for(int i=1;i<=m;i++)
{
int a,b;
cin>>a>>b;
add(a,b);
add(b,a);
}
djs(1);
for(int i=1;i<=n;i++)
cout<<cnt[i]<<endl;
return 0;
}
|
例4.Link with Game Glitch
D-Link with Game Glitch_"蔚来杯"2022牛客暑期多校训练营2 (nowcoder.com)">题目链接
题目大意
给出\(n\)个食材,\(m\)个食谱,为防止无限创造食物,使食谱的产出乘以系数\(w\),问最大的\(w\)
题解
最大最小考虑二分,现在目标是求出check函数,想要使食物不被无限制造,问题等价于食谱图中不存在边权乘积大于1的环,但这样写check函数免不了会爆double,我们考虑转换,将边权都取log的话问题似乎更简单了,转化成了食谱图中不存在正环,套用spfa判正环模板即可
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64 | #include<bits/stdc++.h>
using namespace std;
const int N = 2005;
const double eps = 1e-8;
int head[N], e[N], ne[N], idx = 0;
int f[N];
double dis[N];
double w[N];
bool vis[N];
int n, m;
queue<int> q;
void add(int a, int b, double c) {
e[idx] = b;
w[idx] = c;
ne[idx] = head[a];
head[a] = idx ++ ;
}
bool check(double x) {
memset(vis, false, sizeof(vis));
memset(f, 0, sizeof(f));
while(q.size()) q.pop();
for(int i = 1; i <= n ; i ++ ) {
vis[i] = true;
dis[i] = 0;
q.push(i);
}
while(q.size()) {
int pos = q.front();
q.pop();
vis[pos] = false;
for(int i = head[pos]; i != -1; i = ne[i]) {
int j = e[i];
if(dis[j] < dis[pos] + w[i] + x) {
dis[j] = dis[pos] + w[i] + x;
f[j] = f[pos] + 1;
if(f[j] >= n) return false;
if(!vis[j]) {
q.push(j);
vis[j] = true;
}
}
}
}
return true;
}
int main() {
cin >> n >> m;
memset(head, -1, sizeof(head));
for(int i = 1; i <= m; i ++ ) {
int a, b;
double x, y;
cin >> x >> a >> y >> b;
add(a, b, log(y * 1.0 / x));
}
double l = 0, r = 1.0;
while(l < r - eps) {
double mid = (l + r) / 2.0;
if(check(log(mid)))l = mid;
else r = mid;
}
printf("%.8lf", l);
return 0;
}
|
例5.最优贸易
题目链接
题目描述
C 国有 n 个大城市和 m 条道路,每条道路连接这 n 个城市中的某两个城市。
任意两个城市之间最多只有一条道路直接相连。
这 m 条道路中有一部分为单向通行的道路,一部分为双向通行的道路,双向通行的道路在统计条数时也计为 1 条。
C 国幅员辽阔,各地的资源分布情况各不相同,这就导致了同一种商品在不同城市的价格不一定相同。
但是,同一种商品在同一个城市的买入价和卖出价始终是相同的。
商人阿龙来到 C 国旅游。
当他得知“同一种商品在不同城市的价格可能会不同”这一信息之后,便决定在旅游的同时,利用商品在不同城市中的差价赚一点旅费。
设 C 国 n 个城市的标号从 1∼n,阿龙决定从 1 号城市出发,并最终在 n 号城市结束自己的旅行。
在旅游的过程中,任何城市可以被重复经过多次,但不要求经过所有 n 个城市。
阿龙通过这样的贸易方式赚取旅费:他会选择一个经过的城市买入他最喜欢的商品——水晶球,并在之后经过的另一个城市卖出这个水晶球,用赚取的差价当做旅费。
因为阿龙主要是来 C 国旅游,他决定这个贸易只进行最多一次,当然,在赚不到差价的情况下他就无需进行贸易。
现在给出 n 个城市的水晶球价格,m 条道路的信息(每条道路所连接的两个城市的编号以及该条道路的通行情况)。
请你告诉阿龙,他最多能赚取多少旅费。
注意:本题数据有加强。
输入格式
第一行包含 2 个正整数 n 和 m,中间用一个空格隔开,分别表示城市的数目和道路的数目。
第二行 n 个正整数,每两个整数之间用一个空格隔开,按标号顺序分别表示这 n 个城市的商品价格。
接下来 m 行,每行有 3 个正整数,x,y,z,每两个整数之间用一个空格隔开。
如果 z=1,表示这条道路是城市 x 到城市 y 之间的单向道路;如果 z=2,表示这条道路为城市 x 和城市 y 之间的双向道路。
输出格式
一个整数,表示答案。
数据范围
\(1≤n≤100000 ,\)
\(1≤m≤500000,\)
\(1≤各城市水晶球价格≤100\)
输入样例
| 5 5
4 3 5 6 1
1 2 1
1 4 1
2 3 2
3 5 1
4 5 2
|
输出样例
题解
对于所有的花费,将集合进行划分,我们发现可以划分为以第\(i\)个地点为中转,两边买入卖出的方案之和
对于每个点\(i\)
只要求出
- 从 \(1\) 走到 \(i\) 的过程中,买入水晶球的最低价格 \(dmin[i]\)
- 从 \(i\) 走到 \(n\) 的过程中,卖出水晶球的最高价格 \(dmax[i]\)
最后的结果即为\(max(dmax[i]-dmin[i])\)
接下来就是就上面两个数组
由于不是拓扑图,因此无法使用DP
考虑最短路
对于Dijkstra,有以下反例
如果当前 \(dmin[i]\) 最小的点是 \(5\),那么有可能存在边 \(5-> 6, 6-> 7, 7-> 5\),假设当前 \(dmin[5] = 10\),则有可能存在 \(6\) 的价格是\(11\), 但 \(7\) 的价格是\(3\),那么 \(dmin[5]\) 的值就应该被更新成\(3\),因此当前最小值也不一定是最终最小值
spfa可行
- 对于dmin,只需要求最小路即可
- 对于dmax,建反图后求最大路即可
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82 | #include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 100010, M = 2000010;
int n, m;
int price[N];
int h[N], rh[N], e[M], ne[M], idx;
int dmin[N], dmax[N];
bool st[N];
void add(int *h, int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void spfa(int *d, int start, int *h, bool flag)
{
queue<int> q;
memset(st, 0, sizeof st);
if (flag) memset(d, 0x3f, sizeof dmin);
q.push(start);
st[start] = true;
d[start] = price[start];
while (q.size())
{
int t = q.front();
q.pop();
st[t] = false;
for (int i = h[t]; ~i; i = ne[i])
{
int j = e[i];
if (flag && d[j] > min(d[t], price[j]) || !flag && d[j] < max(d[t], price[j]))
{
if (flag) d[j] = min(d[t], price[j]);
else d[j] = max(d[t], price[j]);
if (!st[j])
{
st[j] = true;
q.push(j);
}
}
}
}
}
int main()
{
scanf("%d%d", &n, &m);
memset(h, -1, sizeof h);
memset(rh, -1, sizeof rh);
for (int i = 1; i <= n; i ++ ) scanf("%d", &price[i]);
while (m -- )
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
add(h, a, b), add(rh, b, a);
if (c == 2) add(h, b, a), add(rh, a, b);
}
spfa(dmin, 1, h, true);
spfa(dmax, n, rh, false);
int res = 0;
for (int i = 1; i <= n; i ++ ) res = max(res, dmax[i] - dmin[i]);
printf("%d\n", res);
return 0;
}
|
