树形DP
概述
树形DP准确的说是一种DP的思想,将DP建立在树状结构的基础上。整体的思路大致就是用树形的结构存储数据。
树形DP的关键和实现方法是dfs;
先找到树根,从树根开始运用dfs递归,跟dfs一样先初始化,然后递归到叶子节点上为止,把最底层的f[i][j]更新完毕,再回来往上走,自底向上地根据题意更新上层的f数组,最后输出答案即可。
例1.没有上司的舞会
题目链接
题目描述
Ural 大学有 N 名职员,编号为 1∼N。
他们的关系就像一棵以校长为根的树,父节点就是子节点的直接上司。
每个职员有一个快乐指数,用整数 Hi 给出,其中 1≤i≤N。
现在要召开一场周年庆宴会,不过,没有职员愿意和直接上司一起参会。
在满足这个条件的前提下,主办方希望邀请一部分职员参会,使得所有参会职员的快乐指数总和最大,求这个最大值。
输入格式
第一行一个整数 N。
接下来 N 行,第 i 行表示 i 号职员的快乐指数 Hi。
接下来 N−1 行,每行输入一对整数 L,K,表示 K 是 L 的直接上司。
输出格式
输出最大的快乐指数。
数据范围
\(1≤N≤6000,\)
\(−128≤Hi≤127\)
输入样例
1
2
3
4
5
6
7
8
9
10
11
12
13
14 | 7
1
1
1
1
1
1
1
1 3
2 3
6 4
7 4
4 5
3 5
|
输出样例
题解
经典题,首先建树+找根,用\(f[i,0]\)表示不选当前职员且其为根结点时的最大快乐指数,\(f[i,1]\)表示选择当前职员且其为根节点时的最大快乐指数,由于选了当前职员后,他的部下就不能再选,所以状态转移方程如下:
- \(f[i,0] = \sum{max(f[j,0], f[j,1])}\)
- \(f[i,1] = \sum{f[j,0]}\)
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38 | #include<bits/stdc++.h>
using namespace std;
const int N = 6005;
int head[N], e[N], ne[N], w[N], idx = 0;
void add(int a, int b) { // 建树
e[idx] = b;
ne[idx] = head[a];
head[a] = idx ++ ;
}
bool vis[N];
int f[N][2];
void dfs(int u) {
f[u][1] = w[u];
for(int i = head[u]; i != -1; i = ne[i]) {
int j = e[i];
dfs(j);
f[u][0] += max(f[j][0], f[j][1]); // 不选的话其子结点可选可不选
f[u][1] += f[j][0]; // 选了的话其子节点都不能选
}
}
int main() {
int n;
cin >> n;
memset(head, -1, sizeof(head));
for(int i = 1; i <= n; i ++ ) cin >> w[i];
for(int i = 1; i <= n - 1; i ++ ) {
int a, b;
cin >> a >> b;
add(b, a);
vis[a] = true;
}
int root = 1;
while(vis[root]) root ++ ; // 找根
dfs(root);
cout << max(f[root][0], f[root][1]);
return 0;
}
|
例2.树的最长路径
题目链接
题目描述
给定一棵树,树中包含 n 个结点(编号1~n)和 n−1 条无向边,每条边都有一个权值。
现在请你找到树中的一条最长路径。
换句话说,要找到一条路径,使得使得路径两端的点的距离最远。
注意:路径中可以只包含一个点。
输入格式
第一行包含整数 n。
接下来 n−1 行,每行包含三个整数 ai,bi,ci,表示点 ai 和 bi 之间存在一条权值为 ci 的边。
输出格式
输出一个整数,表示树的最长路径的长度。
数据范围
\(1≤n≤10000,\)
\(1≤ai,bi≤n,\)
\(−10^5≤ci≤10^5\)
输入样例
| 6
5 1 6
1 4 5
6 3 9
2 6 8
6 1 7
|
输出样例
题解
本题也称树的直径,朴素做法为枚举每条路径的起点与终点,利用倍增求出两点距离,但这样光枚举起点和终点已经\(O(n^2)\)超时,因此转换枚举方式,我们选择枚举中间结点,并且假设其为路径上的最高点,则直径一定在所有结点的最长路径+次长路径当中,只需要预处理出所有点的最长路径和次长路径即可
但上面有个问题,由于是树的形式,最长或次长路径可能是往上经过父节点的,该怎么办呢?其实这种情况在枚举到它的祖先节点时已经考虑完了,这样问题就解决了,代码给出两种dfs写法,分别为有返回值和无返回值
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93 | // 有返回值
#include<bits/stdc++.h>
using namespace std;
const int N = 1e4+5, M = 2e4+4;
int head[N], e[M], ne[M], w[M], idx = 0;
void add(int a, int b, int c)
{
e[idx] = b;
w[idx] = c;
ne[idx] = head[a];
head[a] = idx ++ ;
}
int n;
int res = 0;
int dfs(int u, int fa) {
int d = 0, d1 = 0, d2 = 0;
for(int i = head[u]; i != -1; i = ne[i]) {
int j = e[i];
if(j == fa) continue;
d = dfs(j, u) + w[i];
if(d >= d1) { // 大于最大值
d2 = d1;
d1 = d;
} else if(d > d2) { // 大于次大值
d2 = d;
}
}
res = max(d1 + d2, res);
return d1;
}
int main()
{
cin >> n;
memset(head, -1, sizeof(head));
for(int i = 1; i <= n - 1; i ++ )
{
int a, b, c;
cin >> a >> b >> c;
add(a, b, c);
add(b, a, c);
}
dfs(1, -1);
cout << res << endl;
return 0;
}
// 无返回值
#include<bits/stdc++.h>
using namespace std;
const int N = 1e4 + 5, M = 2 * N;
int head[N], e[M], ne[M], w[M], idx = 0;
int f[N][2]; // f[i][0] 最长 f[i][1] 次长
void add(int a, int b, int c) {
e[idx] = b;
w[idx] = c;
ne[idx] = head[a];
head[a] = idx ++ ;
}
int res = 0;
void dfs(int u, int fa) {
int d = 0;
for(int i = head[u]; i != -1; i = ne[i]) {
int j = e[i];
if(j == fa) continue;
dfs(j, u);
d = f[j][0] + w[i];
if(d >= f[u][0]) {
f[u][1] = f[u][0];
f[u][0] = d;
} else if(d > f[u][1]) {
f[u][1] = d;
}
}
res = max(res, f[u][0] + f[u][1]);
}
int main() {
int n;
cin >> n;
memset(head, -1, sizeof(head));
for(int i = 0; i < n - 1; i ++ ) {
int a, b, c;
cin >> a >> b >> c;
add(a, b, c);
add(b, a, c);
}
dfs(1, -1);
cout << res;
return 0;
}
|
例3.树的中心
题目链接
题目描述
给定一棵树,树中包含 n 个结点(编号1~n)和 n−1 条无向边,每条边都有一个权值。
请你在树中找到一个点,使得该点到树中其他结点的最远距离最近。
输入格式
第一行包含整数 n。
接下来 n−1 行,每行包含三个整数 ai,bi,ci,表示点 ai 和 bi 之间存在一条权值为 ci 的边。
输出格式
输出一个整数,表示所求点到树中其他结点的最远距离。
数据范围
\(1≤n≤10000,\)
$1≤ai,bi≤n,
\(1≤ci≤10^5\)
输入样例
| 5
2 1 1
3 2 1
4 3 1
5 1 1
|
输出样例
题解
和树的直径很相似,但也很不同,首先考虑对一个点需要比较哪些部分
这就是为什么和树的直径很相似但又不同的地方了,书的直径往父节点走的路径在枚举父节点时已经考虑,是因为当时我们考虑的是直径,一条直径可以被拆成不同的最长路径和次长路径,只要直径的最高点不同即可,而本题只是一条路径,不能被拆分,因此需要考虑往上走,我们用d1,d2存当前点往子结点走的最长和次长路径,用up存往父节点走的不经过当前节点的最长路径,使用两个dfs,第一个处理d1和d2,第二个处理up,最后枚举所有的点更新答案就行了
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63 | #include<bits/stdc++.h>
using namespace std;
const int N = 1e4 + 5, M = 2 * N;
int head[N], e[M], ne[M], w[M], idx = 0;
void add(int a, int b, int c) {
e[idx] = b;
w[idx] = c;
ne[idx] = head[a];
head[a] = idx ++ ;
}
int d1[N], d2[N], up[N]; // 最长,次长,经过父节点的最长
int p1[N], p2[N]; // 存父节点经过的子节点
void dfs_d(int u, int fa) {
int d = 0;
for(int i = head[u]; i != -1; i = ne[i]) {
int j = e[i];
if(j == fa) continue;
dfs_d(j, u);
d = d1[j] + w[i];
if(d >= d1[u]) {
d2[u] = d1[u]; p2[u] = p1[u];
d1[u] = d; p1[u] = j;
} else if(d > d2[u]) {
d2[u] = d;
p2[u] = j;
}
}
}
void dfs_u(int u, int fa) {
for(int i = head[u]; i != -1; i = ne[i]) {
int j = e[i];
if(j == fa) continue;
if(p1[u] == j) { // 最长经过当前结点,此时用次长更新
up[j] = max(up[u], d2[u]) + w[i];
} else { // 不经过就用最长更新
up[j] = max(up[u], d1[u]) + w[i];
}
dfs_u(j, u);
}
}
int main() {
int n;
cin >> n;
memset(head, -1, sizeof(head));
for(int i = 0; i < n - 1; i ++ ) {
int a, b, c;
cin >> a >> b >> c;
add(a, b, c);
add(b, a, c);
}
dfs_d(1, -1);
dfs_u(1, -1);
int res = 0x3f3f3f3f;
for(int i = 1; i <= n; i ++ ) { // 枚举所有点
res = min(res, max(up[i], d1[i]));
}
cout << res;
return 0;
}
|
例4.数字转换
题目链接
题目描述
如果一个数 x 的约数之和 y(不包括他本身)比他本身小,那么 x 可以变成 y,y 也可以变成 x。
例如,4 可以变为 3,1 可以变为 7。
限定所有数字变换在不超过 n 的正整数范围内进行,求不断进行数字变换且不出现重复数字的最多变换步数。
输入格式
输入一个正整数 n。
输出格式
输出不断进行数字变换且不出现重复数字的最多变换步数。
数据范围
\(1≤n≤50000\)
输入样例
输出样例
题解
简易版的树的直径,这里简单提一下预处理约束和的方法,不选择枚举每个数的约束,而选择枚举每个数的倍数,时间复杂度为\(O(nlog_n + C)\),C为欧拉常数,建树后用就是求边权为1时树的直径
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57 | #include<bits/stdc++.h>
using namespace std;
const int N = 5e4 + 5, M = 2 * N;
int head[N], e[M], ne[M], idx = 0;
void add(int a, int b) {
e[idx] = b;
ne[idx] = head[a];
head[a] = idx ++ ;
}
int sum[N];
int res = 0;
int d1[N], d2[N]; // 最长与次长
bool vis[N];
void dfs(int u) {
d1[u] = d2[u] = -0x3f3f3f3f;
for(int i = head[u]; i != -1; i = ne[i]) {
int j = e[i];
if(vis[j]) continue;
vis[j] = true;
dfs(j);
int d = d1[j] + 1;
if(d >= d1[u]) {
d2[u] = d1[u];
d1[u] = d;
} else if(d > d2[u]) {
d2[u] = d;
}
}
if(d1[u] == -0x3f3f3f3f) d1[u] = d2[u] = 0; // 叶子节点为0,本题权值大于0可以不用初始化负无穷
res = max(res, d1[u] + (d2[u] == -0x3f3f3f3f ? 0 : d2[u]));
}
int main() {
int n;
cin >> n;
memset(head, -1, sizeof(head));
for(int i = 1; i <= n; i ++ ) {
for(int j = 2 * i; j <= n; j += i) {
sum[j] += i;
}
}
for(int i = 2; i <= n; i ++ ) {
if(sum[i] < i) {
add(sum[i], i);
add(i, sum[i]);
}
}
for(int i = 1; i <= n; i ++ ) {
if(!vis[i]) {
vis[i] = true;
dfs(i);
}
}
cout << res;
return 0;
}
|
例5.战略游戏
题目链接
题目描述
鲍勃喜欢玩电脑游戏,特别是战略游戏,但有时他找不到解决问题的方法,这让他很伤心。
现在他有以下问题。
他必须保护一座中世纪城市,这条城市的道路构成了一棵树。
每个节点上的士兵可以观察到所有和这个点相连的边。
他必须在节点上放置最少数量的士兵,以便他们可以观察到所有的边。
你能帮助他吗?
例如,下面的树:
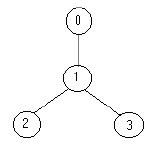
只需要放置 1 名士兵(在节点 1 处),就可观察到所有的边。
输入格式
输入包含多组测试数据,每组测试数据用以描述一棵树。
对于每组测试数据,第一行包含整数 N,表示树的节点数目。
接下来 N 行,每行按如下方法描述一个节点。
节点编号:(子节点数目) 子节点 子节点 …
节点编号从 0 到 N−1,每个节点的子节点数量均不超过 10,每个边在输入数据中只出现一次。
输出格式
对于每组测试数据,输出一个占据一行的结果,表示最少需要的士兵数。
数据范围
\(0<N≤1500 ,\)
一个测试点所有 N 相加之和不超过 \(300650\)。
输入样例
| 4
0:(1) 1
1:(2) 2 3
2:(0)
3:(0)
5
3:(3) 1 4 2
1:(1) 0
2:(0)
0:(0)
4:(0)
|
输出样例
题解
没有上司的舞会我扩展,与其不同的是若父节点选择,其子节点可选可不选,父节点未选择,子节点必选,状态转移方程如下:
- \(f[i,1]=\sum min(f[j,0],f[j,1]\)
- \(f[i,0]=\sum f[j,1]\)
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97 | // 无返回值
#include<bits/stdc++.h>
using namespace std;
const int N = 1505;
int head[N], e[N], ne[N], idx = 0;
void add(int a, int b) {
e[idx] = b;
ne[idx] = head[a];
head[a] = idx ++ ;
}
bool vis[N];
int f[N][2];
void dfs(int u) {
f[u][0] = 0;
f[u][1] = 1;
for(int i = head[u]; i != -1; i = ne[i]) {
int j = e[i];
dfs(j);
f[u][0] += f[j][1];
f[u][1] += min(f[j][0], f[j][1]);
}
}
int main() {
int n;
while(scanf("%d", &n) != -1) {
idx = 0;
memset(head, -1, sizeof(head));
memset(vis, false, sizeof(vis));
for(int i = 0; i < n; i ++ ) {
int a;
int k;
scanf("%d:(%d)", &a, &k);
for(int j = 0; j < k; j ++ ) {
int b;
scanf("%d", &b);
add(a, b);
vis[b] = true;
}
}
int root = 0;
while(vis[root]) root ++ ;
dfs(root);
cout << min(f[root][0],f[root][1]) << endl;
}
return 0;
}
//有返回值
#include<bits/stdc++.h>
using namespace std;
const int N = 1505;
int head[N], e[N], ne[N], idx = 0;
void add(int a, int b) {
e[idx] = b;
ne[idx] = head[a];
head[a] = idx ++ ;
}
bool vis[N];
int f[N][2];
int dfs(int u, int t) {
if(f[u][t] != -1) return f[u][t];
if(t == 0) f[u][t] = 0;
else f[u][t] = 1;
for(int i = head[u]; i != -1; i = ne[i]) {
int j = e[i];
if(t == 0) f[u][t] += dfs(j, 1);
else f[u][t] += min(dfs(j, 1), dfs(j, 0));
}
return f[u][t];
}
int main() {
int n;
while(scanf("%d", &n) != -1) {
idx = 0;
memset(head, -1, sizeof(head));
memset(vis, false, sizeof(vis));
memset(f, -1, sizeof(f));
for(int i = 0; i < n; i ++ ) {
int a;
int k;
scanf("%d:(%d)", &a, &k);
for(int j = 0; j < k; j ++ ) {
int b;
scanf("%d", &b);
add(a, b);
vis[b] = true;
}
}
int root = 0;
while(vis[root]) root ++ ;
cout << min(dfs(root, 0), dfs(root, 1)) << endl;
}
return 0;
}
|
例6.皇宫看守
题目链接
题目描述
太平王世子事件后,陆小凤成了皇上特聘的御前一品侍卫。
皇宫各个宫殿的分布,呈一棵树的形状,宫殿可视为树中结点,两个宫殿之间如果存在道路直接相连,则该道路视为树中的一条边。
已知,在一个宫殿镇守的守卫不仅能够观察到本宫殿的状况,还能观察到与该宫殿直接存在道路相连的其他宫殿的状况。
大内保卫森严,三步一岗,五步一哨,每个宫殿都要有人全天候看守,在不同的宫殿安排看守所需的费用不同。
可是陆小凤手上的经费不足,无论如何也没法在每个宫殿都安置留守侍卫。
帮助陆小凤布置侍卫,在看守全部宫殿的前提下,使得花费的经费最少。
输入格式
输入中数据描述一棵树,描述如下:
第一行 n,表示树中结点的数目。
第二行至第 n+1 行,每行描述每个宫殿结点信息,依次为:该宫殿结点标号 i,在该宫殿安置侍卫所需的经费 k,该结点的子结点数 m,接下来 m 个数,分别是这个结点的 m 个子结点的标号 r1,r2,…,rm。
对于一个 n 个结点的树,结点标号在 1 到 n 之间,且标号不重复。
输出格式
输出一个整数,表示最少的经费。
数据范围
\(1≤n≤1500\)
输入样例
| 6
1 30 3 2 3 4
2 16 2 5 6
3 5 0
4 4 0
5 11 0
6 5 0
|
输出样例
题解
上题要求观察到所有的边,本题要求观察到所有的点,此时考虑像上题一样,每个点有无防守卫这两个状态是否足够,讨论当前点不放置守卫的情况:
- 当前点不放守卫但被父节点观察到,则它的子节点可以放置守卫,也可以不放置守卫
- 当前点不放守卫但未被父节点观察到,则它的子节点必须放置守卫
因此对于上述情况来看两个状态是不够的
我们定义:
- \(f[i,0]\)为不放置守卫但被父节点观察到
- \(f[i,1]\)为不放置守卫也未被父节点观察到
- \(f[i,1]\)为放置守卫
状态转移方程如下:
- \(f[i,0]=\sum min(f[j,1],f[j,2])\)
- \(f[i,1]=min(f[i, 1], f[k, 2] + \sum_{j \ne k} min(f[j, 1],f[j, 2]))\) (其中一点放守卫观察,其余点可放可不放,取最小)
- \(f[i,2]=\sum min(f[j,0], f[j,1],f[j,2])\)
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57 | //f[i, 0] 不放哨兵被父节点观察到 f[i, 0] += min(f[j, 1], f[j, 2])
//f[i, 1] 不放哨兵被子节点观察到 f[i, 1] = min(f[k, 2], sigema min(f[j, 1], f[j, 2]))
//f[i, 2] 放哨兵 f[i, 2] += min(f[j, 1], f[j, 2], f[j, 0])
#include<bits/stdc++.h>
using namespace std;
const int N = 1505, M = 2 * N;
int head[N], e[M], ne[M], idx = 0;
int w[N];
bool vis[N];
void add(int a, int b) {
e[idx] = b;
ne[idx] = head[a];
head[a] = idx ++ ;
}
int f[N][3];
void dfs(int u) {
f[u][0] = 0;
f[u][1] = 1e9;
f[u][2] = w[u];
for(int i = head[u]; i != -1; i = ne[i]) {
int j = e[i];
dfs(j);
f[u][0] += min(f[j][1], f[j][2]);
f[u][2] += min(f[j][0], min(f[j][1], f[j][2]));
}
for(int i = head[u]; i != -1; i = ne[i]) {
int j = e[i];
f[u][1] = min(f[u][1], f[j][2] + f[u][0] - min(f[j][1], f[j][2]));
}
}
int main() {
int n;
cin >> n;
memset(head, -1, sizeof(head));
for(int i = 1; i <= n; i ++ ) {
int a, k, tt;
cin >> a;
cin >> k;
w[a] = k;
cin >> tt;
for(int j = 1; j <= tt; j ++ ) {
int b;
cin >> b;
add(a, b);
vis[b] = true;
}
}
memset(f, -1, sizeof(f));
int root = 1;
while(vis[root]) root ++ ;
dfs(root);
cout << min(f[root][1], f[root][2]);
return 0;
}
|
