跳转至

区间DP

概述

区间dp就是利用了分治的思想，将整个区间不断的拆分一下，将一个区间[l,r]分成[l,k] [k+1,r]，然后再对[l,k]和[k+1,r]进行类似的拆分，直到拆分成最小的区间，通过对每个小区间算出最小或者最大代价，再通过将这些小区间组合成一个更大的区间，哪种组合方式最优，则就是所求解。解题为三部分+最后一步+边界情况。

例1.石子合并

题目链接

题目描述 设有 N 堆石子排成一排，其编号为 1，2，3，…，N。

每堆石子有一定的质量，可以用一个整数来描述，现在要将这 N 堆石子合并成为一堆。

每次只能合并相邻的两堆，合并的代价为这两堆石子的质量之和，合并后与这两堆石子相邻的石子将和新堆相邻，合并时由于选择的顺序不同，合并的总代价也不相同。

例如有 4 堆石子分别为 1 3 5 2， 我们可以先合并 1、2 堆，代价为 4，得到 4 5 2， 又合并 1，2 堆，代价为 9，得到 9 2 ，再合并得到 11，总代价为 4+9+11=24；

如果第二步是先合并 2，3 堆，则代价为 7，得到 4 7，最后一次合并代价为 11，总代价为 4+7+11=22。

问题是：找出一种合理的方法，使总的代价最小，输出最小代价。

输入格式

第一行一个数 N 表示石子的堆数 N。

第二行 N 个数，表示每堆石子的质量(均不超过 1000)。

输出格式

输出一个整数，表示最小代价。

数据范围

\(1≤N≤300\)

输入样例

1
2
4
1 3 5 2

输出样例

1
22

题解

区间DP的状态定义一般为一个范围，我们令\(f[l,r]\)为合并\(l-r\)范围内的石子能获得的最小代价，根据最后一步合并的不同，可以划分为若干个部分，状态转移方程很容易可以表示为\(f[l,r]=min(f[l,k]+f[k + 1,r] + (w[l]+w[l+1]...+w[r]), f[l,r])\)，其中k为最后一步合并的端点,这里\(w[l]+...w[r]\)可以用前缀和优化

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include<bits/stdc++.h>
using namespace std;
const int N=305;
int dp[N][N];
int a[N],sum[N];
int main()
{
    int n;
    cin>>n;
    for(int i=1;i<=n;i++) cin>>a[i];
    for(int i=1;i<=n;i++) sum[i]=sum[i-1]+a[i];
    memset(dp,0x3f,sizeof(dp));
    for(int i=1;i<=n;i++) dp[i][i]=0;
    for(int len=1;len<=n;len++)
    {
        for(int i=1;i<=n;i++)
        {
            if(i+len-1>n) break;
            int l=i,r=i+len-1;
            for(int k=l;k<=r;k++)
            {
                dp[l][r]=min(dp[l][r],dp[l][k]+dp[k+1][r]+sum[r]-sum[l-1]);
            }
        }
    }
    cout<<dp[1][n]<<endl;
    return 0;
}

例2.环形石子合并

题目链接

题目描述

将 n 堆石子绕圆形操场排放，现要将石子有序地合并成一堆。

规定每次只能选相邻的两堆合并成新的一堆，并将新的一堆的石子数记做该次合并的得分。

请编写一个程序，读入堆数 n 及每堆的石子数，并进行如下计算：

  • 选择一种合并石子的方案，使得做 n−1 次合并得分总和最大。
  • 选择一种合并石子的方案，使得做 n−1 次合并得分总和最小。

输入格式

第一行包含整数 n，表示共有 n 堆石子。

第二行包含 n 个整数，分别表示每堆石子的数量。

输出格式

输出共两行：

第一行为合并得分总和最小值，

第二行为合并得分总和最大值。

数据范围

\(1≤n≤200\)

输入样例

1
2
4
4 5 9 4

输出样例

1
2
43
54

题解

与朴素版相比，多了一个破环成链的过程，由于是个环，n堆石子就有n个空隙，若按照空隙断开可以有n种断法，由于环断开后个数仍然为n个，于是不难想到可以在原n堆石子后面补上n个，从前n堆开始分别对应一种断法，最后在这些断法中取最小值(或最大值)，而每种断法使用朴素版的做法即可

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include<bits/stdc++.h>
using namespace std;
const int N = 405, INF = 0x3f3f3f3f;
int f[N][N], g[N][N];
int a[N];
int sum[N];
int main() {
    int n;
    cin >> n;
    for(int i = 1; i <= n; i ++ ) {
        cin >> a[i];
        a[i + n] = a[i];
    }

    for(int i = 1; i <= 2 * n; i ++ ) sum[i] = sum[i - 1] + a[i];
    memset(f, 0x3f, sizeof(f));
    memset(g, -0x3f, sizeof(g));
    for(int i = 1; i <= 2 * n; i ++ ) f[i][i] = g[i][i] = 0;
    for(int len = 2; len <= n; len ++ ) {
        for(int l = 1; l + len - 1 <= 2 * n; l ++ ) {
            int r = l + len - 1;
            for(int k = l; k <= r; k ++ ) {
                f[l][r] = min(f[l][r], f[l][k] + f[k + 1][r] + sum[r] - sum[l - 1]);
                g[l][r] = max(g[l][r], g[l][k] + g[k + 1][r] + sum[r] - sum[l - 1]);
            }
        }
    }

    int minx = INF, maxx = -INF;
    for(int i = 1; i <= n; i ++ ) {
        minx = min(minx, f[i][i + n - 1]);
        maxx = max(maxx, g[i][i + n - 1]);
    }
    cout << minx << endl << maxx;
    return 0;
}

例3.能量项链

题目链接

题目描述

在 Mars 星球上，每个 Mars 人都随身佩带着一串能量项链，在项链上有 N 颗能量珠。

能量珠是一颗有头标记与尾标记的珠子，这些标记对应着某个正整数。

并且，对于相邻的两颗珠子，前一颗珠子的尾标记一定等于后一颗珠子的头标记。

因为只有这样，通过吸盘（吸盘是 Mars 人吸收能量的一种器官）的作用，这两颗珠子才能聚合成一颗珠子，同时释放出可以被吸盘吸收的能量。

如果前一颗能量珠的头标记为 m，尾标记为 r，后一颗能量珠的头标记为 r，尾标记为 n，则聚合后释放的能量为 m×r×n（Mars 单位），新产生的珠子的头标记为 m，尾标记为 n。

需要时，Mars 人就用吸盘夹住相邻的两颗珠子，通过聚合得到能量，直到项链上只剩下一颗珠子为止。

显然，不同的聚合顺序得到的总能量是不同的，请你设计一个聚合顺序，使一串项链释放出的总能量最大。

例如：设 N=4，4 颗珠子的头标记与尾标记依次为 (2，3)(3，5)(5，10)(10，2)。

我们用记号 ⊕ 表示两颗珠子的聚合操作，(j⊕k) 表示第 j，k 两颗珠子聚合后所释放的能量。则

第 4、1 两颗珠子聚合后释放的能量为：(4⊕1)=10×2×3=60。

这一串项链可以得到最优值的一个聚合顺序所释放的总能量为 ((4⊕1)⊕2)⊕3)=10×2×3+10×3×5+10×5×10=710。

输入格式

输入的第一行是一个正整数 N，表示项链上珠子的个数。

第二行是 N 个用空格隔开的正整数，所有的数均不超过 1000，第 i 个数为第 i 颗珠子的头标记，当 i < N 时，第 i 颗珠子的尾标记应该等于第 i+1 颗珠子的头标记，第 N 颗珠子的尾标记应该等于第 1 颗珠子的头标记。

至于珠子的顺序，你可以这样确定：将项链放到桌面上，不要出现交叉，随意指定第一颗珠子，然后按顺时针方向确定其他珠子的顺序。

输出格式

输出只有一行，是一个正整数 E，为一个最优聚合顺序所释放的总能量。

数据范围

\(4≤N≤100,\)

\(1≤E≤2.1×109\)

输入样例

1
2
4
2 3 5 10

输出样例

1
710

题解

环形问题，首先破环成链，参考环形石子合并的方法，本题与环形石子合并的不同点在于每一堆既有头也有尾，因此对于堆数为n的石子实际长度应该为n+1，所以本题就是在长度为n+1的石子堆中做环形石子合并问题，第n+1和第1个一样，长度为1不存在，因此可以从2开始枚举，注意一个小坑，在枚举最后一步时不能选择一个珠子的同一端，即k范围为l+1到r-1

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include<bits/stdc++.h>
using namespace std;
const int N = 205;
int dp[N][N];
int a[N];
int main() {
    int n;
    cin >> n;
    for(int i = 1; i <= 2 * n; i ++ ) {
        cin >> a[i];
        a[i + n] = a[i];
    }

    for(int len = 2; len <= n + 1; len ++ ) {
        for(int l = 1; l + len - 1 <= 2 * n; l ++ ) {
            int r = l + len - 1;
            for(int k = l + 1; k <= r - 1; k ++ ) {
                dp[l][r] = max(dp[l][r], dp[l][k] + dp[k][r] + a[l] * a[r] * a[k]);
            }
        }
    }
    int res = 0;
    for(int i = 1; i <= n; i ++ ) {
        res = max(res, dp[i][i + n]);
    }
    cout << res;
    return 0;
}

例4.凸多边形的划分

题目链接

题目描述

给定一个具有 N 个顶点的凸多边形，将顶点从 1 至 N 标号，每个顶点的权值都是一个正整数。

将这个凸多边形划分成 N−2 个互不相交的三角形，对于每个三角形，其三个顶点的权值相乘都可得到一个权值乘积，试求所有三角形的顶点权值乘积之和至少为多少。

输入格式

第一行包含整数 N，表示顶点数量。

第二行包含 N 个整数，依次为顶点 1 至顶点 N 的权值。

输出格式

输出仅一行，为所有三角形的顶点权值乘积之和的最小值。

数据范围

\(N≤50,\)

数据保证所有顶点的权值都小于\(10^9\)

输入样例

1
2
5
121 122 123 245 231

输出样例

1
12214884

题解

我们枚举三角形中的一条边，设\(f[l,r]\)为所有由\([l,l+1],[l+1,l+2],...[r-2,r-1],[r-1,r],[r-l]\)这些边组成的四边形划分成三角形方案的最小值，根据最后一步即除\(l,r\)这两个点外三角形另一个顶点的位置确定状态转移方程，可以发现第三个点可以取到\((l,r)\)内的所有点，于是\(f[l,r]=min(f[l,r],f[l,k]+f[k,r]+w[l]*w[k]*w[r]\)，看上去和上题转移方程一样，但本题长度为n并且不需要破环就能枚举到所有线段，数据范围很大，需要使用高精度

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 55, M = 100;
int dp[N][N][M];
int a[N];
int n;
void add(int a[], int b[]) {
    int c[M];
    memset(c, 0, sizeof(c));
    for(int i = 0, t = 0; i < M; i ++ ) {
        t += a[i] + b[i];
        c[i] = t % 10;
        t /= 10;
    }
    memcpy(a, c, sizeof(c));
}

void mul(int a[], int b) {
    int c[M];
    memset(c, 0, sizeof(c));
    int t = 0;
    for(int i = 0; i < M; i ++ ) {
        t += a[i] * b;
        c[i] = t % 10;
        t /= 10;
    }

    memcpy(a, c, sizeof(c));
}


int cmp(int a[], int b[]) {
    for(int i = M - 1; i >= 0; i -- ) {
        if(a[i] > b[i]) return 1;
        else if(a[i] < b[i]) return -1;
    }
    return 0;
}


void print(int a[]) {
    int k = M - 1;
    while(!a[k] && k) k -- ;
    while(k >= 0) cout << a[k -- ];
    cout << endl;
}
signed main() {
    cin >> n;
    for(int i = 1; i <= n; i ++ ) {
        cin >> a[i];
    }
    int tmp[M];
    for(int len = 3; len <= n; len ++ ) {
        for(int l = 1; l + len - 1 <= n; l ++ ) {
            int r = l + len - 1;
            for(int i = 0; i < M; i ++ ) dp[l][r][i] = 9;
            for(int k = l + 1; k < r; k ++ ) {
                // dp[l][r] = min(dp[l][r], dp[l][k] + dp[k][r] + a[l] * a[k] * a[r]);
                memset(tmp, 0, sizeof(tmp));
                tmp[0] = a[l];
                mul(tmp, a[k]);
                mul(tmp, a[r]);
                add(tmp, dp[l][k]);
                add(tmp, dp[k][r]);
                if(cmp(dp[l][r], tmp) > 0) memcpy(dp[l][r], tmp, sizeof(tmp));
            }
        }
    }
    print(dp[1][n]);
    return 0;
}

例5.加分二叉树

题目描述

设一个 n 个节点的二叉树 tree 的中序遍历为（1,2,3,…,n），其中数字 1,2,3,…,n 为节点编号。

每个节点都有一个分数（均为正整数），记第 i 个节点的分数为 di，tree 及它的每个子树都有一个加分，任一棵子树 subtree（也包含 tree 本身）的加分计算方法如下：     

subtree的左子树的加分 × subtree的右子树的加分 ＋ subtree的根的分数 

若某个子树为空，规定其加分为 1。

叶子的加分就是叶节点本身的分数，不考虑它的空子树。

试求一棵符合中序遍历为（1,2,3,…,n）且加分最高的二叉树 tree。

要求输出： 

（1）tree的最高加分 

（2）tree的前序遍历

输入格式

第 1 行：一个整数 n，为节点个数。 

第 2 行：n 个用空格隔开的整数，为每个节点的分数（0<分数<100）。

输出格式

第 1 行：一个整数，为最高加分（结果不会超过int范围）。     

第 2 行：n 个用空格隔开的整数，为该树的前序遍历。如果存在多种方案，则输出字典序最小的方案。

数据范围

\(n<30\)

输入样例

1
2
5
5 7 1 2 10

输出样例

1
2
145
3 1 2 4 5

题解

由于每一颗树的中序遍历在序列中时连续的一段，根据以往区间DP将其分成三部分的规律，很容易想到令\(f[l,r]\)为中序遍历为\(l-r\)的二叉树方案的分数最大值，这里的最后一步是根结点的位置，假设为k，则状态转移方程为\(f[l,r]=max(f[l,r],f[l,k-1] \times f[k+1,r]+w[k])\)

注意边界情况

  • 当没有子树时分数为自身值
  • 当没有一颗子树时，没有的子树权值为1

本题还要求输出字典序最小的前序遍历，由于前序遍历优先输出根节点，而根节点又为下标，于是想到根结点越靠前越好，即找到第一个满足最大值的数，之后遇到相同分数不进行\(f[l,r]\)的更新

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
// f[l][r]为中序遍历为l-r的二叉树的分数最大值
// g[l][r]表示根

#include<bits/stdc++.h>
using namespace std;
const int N = 35;
int a[N];
int f[N][N];
int g[N][N];
void dfs(int l, int r) {
    if(l > r) return ;
    int root = g[l][r];
    cout << root << " ";
    dfs(l, root -  1);
    dfs(root + 1, r);
}
int main() {
    int n;
    cin >> n;
    for(int i = 1; i <= n; i ++ ) cin >> a[i];
    for(int i = 1; i <= n; i ++ ) {
        f[i][i] = a[i];
        g[i][i] = i;
    }

    for(int len = 2; len <= n; len ++ ) {
        for(int l = 1; l + len - 1 <= n; l ++ ) {
            int r = l + len - 1;
            for(int k = l; k <= r; k ++ ) {
                int left = (k == l ? 1 : f[l][k - 1]);
                int right = (k == r ? 1 : f[k + 1][r]);
                int score = left * right + a[k];
                if(score > f[l][r]) { // 字典序最小要求根的位置为最左边
                    f[l][r] = score;
                    g[l][r] = k;
                }
            }
        }
    }

    cout << f[1][n] << endl;
    dfs(1, n);
    return 0;
}

例6.棋盘分割

题目描述

将一个 8×8 的棋盘进行如下分割：将原棋盘割下一块矩形棋盘并使剩下部分也是矩形，再将剩下的部分继续如此分割，这样割了 (n−1) 次后，连同最后剩下的矩形棋盘共有 n 块矩形棋盘。(每次切割都只能沿着棋盘格子的边进行)

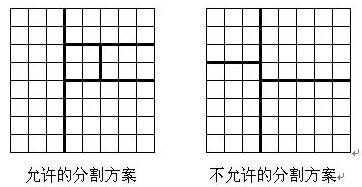
原棋盘上每一格有一个分值，一块矩形棋盘的总分为其所含各格分值之和。

现在需要把棋盘按上述规则分割成 n 块矩形棋盘，并使各矩形棋盘总分的均方差最小。

均方差formula.png ，其中平均值lala.png ，xi 为第 i 块矩形棋盘的总分。

请编程对给出的棋盘及 n，求出均方差的最小值。

输入格式 第 1 行为一个整数 n。

第 2 行至第 9 行每行为 8 个小于 100 的非负整数，表示棋盘上相应格子的分值。每行相邻两数之间用一个空格分隔。

输出格式

输出最小均方差值（四舍五入精确到小数点后三位）。

数据范围

\(1<n<15\)

输入样例

1
2
3
4
5
6
7
8
9
3
1 1 1 1 1 1 1 3
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 0
1 1 1 1 1 1 0 3

输出样例

1
1.633

题解

设\(f[x1][y1][x2][y2][k]\)为左端点为\((x1,y1)\)，右端点为\((x2,y2)\)的矩阵划分为k部分的均方差的最小值，发现若要使所有部分在切的过程中都能为矩形，只有横切到底和竖切到底两种方法，本题使用记忆化搜索来写

状态转移方程如下:

  • 横切:\(f[x1][y1][x2][y2][k]=min(f[x1][y1][x2][i][k-1]+get(x1,i+1,x2,y2),\) \(f[x1][i+1][x2][y2][k-1]+get(x1,y1,x2,i),f[x1][y1][x2][y2][k])\)
  • 竖切:\(f[x1][y1][x2][y2][k]=min(f[x1][y1] [x2][i][k-1]+get(x1, i + 1, x2, y2),\) \(f[x1][i+1][x2][y2][k-1]+get(x1, y1, x2, i),f[x1][y1][x2][y2][k])\)

利用二维前缀和继续优化

代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include<bits/stdc++.h>
using namespace std;
const int N = 10, M = 16;
double s[N][N];
double f[M][M][M][M][N];
double X;
int n;

double get(int x1, int y1, int x2, int y2) {
    double sum = s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1];
    sum -= X;
    return sum * sum / n;
}

double dfs(int x1, int y1, int x2, int y2, int k) {
    double &v = f[x1][y1][x2][y2][k];
    if(v >= 0) return v;
    if(k == 1) return get(x1, y1, x2, y2);

    v = 0x3f3f3f3f;
    for(int i = x1; i < x2; i ++ ) { // 横
        v = min(v, dfs(x1, y1, i, y2, k - 1) + get(i + 1, y1, x2, y2));
        v = min(v, dfs(i + 1, y1, x2, y2, k - 1) + get(x1, y1, i, y2));
    }

    for(int i = y1; i < y2; i ++ ) { // 竖
        v = min(v, dfs(x1, y1, x2, i, k - 1) + get(x1, i + 1, x2, y2));
        v = min(v, dfs(x1, i + 1, x2, y2, k - 1) + get(x1, y1, x2, i));
    }

    return v;
}

int main() {
    cin >> n;
    for(int i = 1; i <= 8; i ++ ) {
        for(int j = 1; j <= 8; j ++ ) {
            cin >> s[i][j];
            s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
        }
    }

    X = s[8][8] / n;
    memset(f, -1, sizeof(f));
    printf("%.3lf", sqrt(dfs(1, 1, 8, 8, n)));
    return 0;
}